The Monty Hall problem explained
"If something doesn't make sense it means that one of your assumptions is wrong" - Gregory House
If you want to present to your friend a problem that he will probably get wrong, you do not have to look for advanced physics problems, google interview questions or Sherlock Holmes mysteries. No...it is enough to look at a family friendly game show that makes you pick a door.
Of course the previous paragraph alludes to the (in)famous Monty Hall Problem, named after the original host of the Let's make a deal TV show. He presented to the contestants a similar challenge (I do not know how true this is since I was not around back then). It was formulated by a reader of Parade magazine and answered by Marilyn vos Savant.

It is renowned not only because of its counter-intuitive answer, but also because of its reputation of making even people with a certain certified intellectual value (e.g. a PhD degree) disagree with the answer once it is revealed. Here are some samples of the original letters Savant received after she published her answer (you can find more on her site):
May I suggest that you obtain and refer to a standard textbook on probability before you try to answer a question of this type again? - Charles Reid, Ph.D. University of Florida
Maybe women look at math problems differently than men. - Don Edwards Sunriver, Oregon
I am sure you will receive many letters on this topic from high school and college students. Perhaps you should keep a few addresses for help with future columns. - W. Robert Smith, Ph.D. Georgia State University
I am sure everyone who tried to present this problem to their acquaintances got similar responses.
What I will do in this article is present the problem and answer it. Most importantly, I will then try to show as many as possible explanations with the hope that at least one will trigger the illuminating "Aha!" moment that I think is so wonderful when trying to understand a tricky subject.
The Monty Hall Problem
The story goes like this:
This is it. The famous Monty Hall problem resumes to the simple question: Is it better to switch or to stay with your original choice ?(of course assuming you want to win the car, although I can't blame those who would choose the goat over the car).
Think of what you would do and go on and read the next of the article afterwards.
The solution

Maybe surprisingly for some, the answer is that it is always better to switch. In fact, you double your chances of winning if you switch rather than stay with you original choice. With switching you have 66.6% chance of winning the car, while not switching gives you a 33.3% chance of winning.
Explanations Ranked
I will next rank all the explanations that I am aware of. Please post other ones in the comments if you have good ones.
5. Information Matters
Many people have the misconception that since there are two doors, then the chances of either having the car is 50%. That is because it is so deeply embedded in the human intuition that the probabilities are evenly distributed among the number of unknowns. This is also reinforced by the fact that if a player switches 50% of the time, he will indeed win 50% of the time.
One of the sources for this mistake is that people disregard the fact that information was actually given to them by Monty Hall when he reveals one of the goats. When you first pick your door you have a \(\frac{1}{3}\) chance of getting the right door. Then when Monty opens one of the remaining two doors, he will reveal a goat. Basically the remaining door has defeated in the battle of probability the one with the goat and stole its odds, becoming a \(\frac{2}{3}\) favorite against your door.
4. Take all possible cases
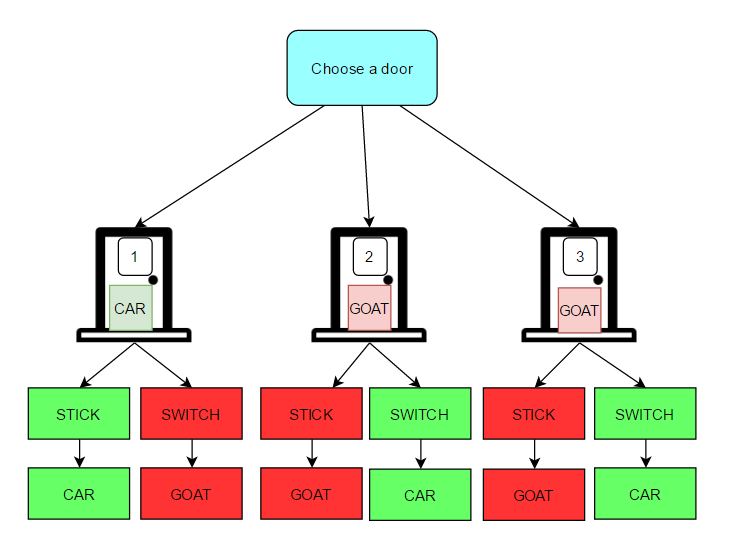
An easy way to explain this will be to ask the non believer to take all the possible cases and see what is the result. This is illustrated in the simple diagram bellow:
As you can see, if you do not switch, you can only win if you initially picked the car. If you switch, you win if you picked the goat initially. The latter is twice as likely to happen than the former, since there are 2 goats in the game and only one car.
3. Multiple doors
This explanation is where most of the people realize that they were actually fooled by Monty's shenanigans. Imagine that instead of 3 doors there are 100 doors. You still pick 1 of them randomly with the chance of it hiding the car being 1%. From the remaining 99 doors, Monty opens all of them except one. Do you still think there is a 50% chance between your door and the remaining door ? Don't you get the feeling that there is something special about that door not being opened, while 98 other doors were opened ? Remember your door does not have the same special status since it was protected from being opened by the fact that you chose it and Monty was not allowed to open it.
2. Try it yourself
Another great way to convince you of the truth is to try this experiment. Luckily it is very easy to do so. You can go to this link and play the game. The site aggregates the results of all those who played. You will see that the theoretical result matches with the real one.
1. Doing the math
Now we get to the serious part.
As a warning, skip this part if you are not a fan of probabilities and math. I am not a mathematician, so any feedback regarding the rigorosity of this proof is welcomed. Still reading? Good. Let's do this.

This is actually not trivial, even though it does look like a very simple problem at first glance. The main difficulty comes in defining the right model to do our analysis, so we will start with that.
We will use random variables to model the possible choices in this game. There are 4 that have a role here:
- D: the the door containing the car.
- P: the first door selected by the player.
- H: the door opened by the host.
- X: the final door selected by the player.
Since each variables will represent a door, they can only have as possible values the doors identifiers: 1, 2 and 3(or A,B and C as in the pictures, but it is a little bit clearer with numbers).
We will now impose some restrictions based on some common sense:
- The first thing you will notice is that the host cannot open a door that is selected by the player, so P ≠ H and X ≠ H.
- The second thing to notice, and this is very important, is that the host will not open the door with the car. This is the main source of controversy for some that assume that he can open the door with the car. To be fair the original enunciation of the problem is not very clear about this aspect. In conclusion D ≠ H.
It is fair to assume that the car is randomly hidden behind one of the doors, which leads to a uniform distribution with an equal chance for each door to hide the car. Taking that into account, the probability density function of the door containing the car is:
\[P(D = i)=\frac{1}{3}\ for\ i∈\{1,2,3\} \]
The player will first choose randomly a door, since he has no information that will modify the decision in favor of one of the doors. This leads to the uniform distribution and the probability density function of his first choice will be as follows:
\[P(P = j)=\frac{1}{3}\ for\ j∈\{1,2,3\} \]
Next we define the conditional density function of the door the host opens, in other words how probable is that he will open one of the doors given that he knows where the car is and what door the player first chose. Recall from our restrictions that the host cannot open the door chosen by the player or the door where the car is. If the player chooses the door with the car, the host can open any of the two other doors, but if the player chooses a door with a goat, the host is obligated to open the only other door that does not contain the car. In conclusion:
\[
P(H = k ∣ D = i, P = j) = \left\{
\begin{array}{ll}
1,\ i≠j,i≠k,k≠j \\
\frac{1}{2},\ i=j,k≠i \\
0,\ k=i,k=j
\end{array}
\right. for\ i,j,k∈\{1,2,3\}
\]
The probability density function of the player's second choice is conditioned by the knowledge he has so far (i.e. what door he choose in the first step and what door the host opened). Recall that (obviously) the player cannot choose the door that is open. Here we introduce a parameter s to indicate how probable is that the player will switch his door for the one offered by Monty Hall. In the extreme cases this will be:
- If the player never switches, s=0
- If the player always switches, s=1
Taking all these facts into account we get the following:
\[
P(X = l ∣ P = j, H = k) = \left\{
\begin{array}{ll}
s,\ l≠j,l≠k,k≠j \\
1-s,\ l=j,k≠j \\
0,\ k=l,k=j
\end{array}
\right. for\ l,j,k∈\{1,2,3\}\ with\ j≠k
\]
We will now unite all these functions in one giant one that will be able to describe any event that happens in this game that we modeled mathematically. Using the multiplication rule of conditional probabilities, we have the following:
\(P(D=i,P=j,H=k,X=l)=
P(D=i) \times P(P=j) \times P(H=k∣D=i,P=j) \times P(X=l∣P=j,H=k)\)
\[i,j,k,l∈\{1,2,3\}\]
Remember that the first two terms are constant so the formula above becomes:
\(P(D=i,P=j,H=k,X=l)=
\frac{1}{9} \times P(H=k∣D=i,P=j) \times P(X=l∣P=j,H=k)\)
\[i,j,k,l∈\{1,2,3\}\]
We are almost done. The only remaining thing in our setup is to define our winning condition. That is that the second door choice of the player will be the same as the door that is hiding the car, so X=D.
Now it is calculating time. We have to sum the probabilities of all scenarios where our winning condition holds. If we take all possible terms it will be quite a long sum, so we will do some simplifications. First we directly remove all terms of our sum that are zero, those being the impossible scenarios(e.g. the host opens the same door as where the car is). Let us take now all the winning scenarios for the winning door being door number 1 (D=1) using the above defined functions:
\(\frac{1}{9} \times P(H=2∣D=1,P=1) \times P(X=1∣P=1,H=2) = \frac{1}{9}\times\frac{1}{2}\times(1-s)=\frac{1-s}{18}\)
\(\frac{1}{9} \times P(H=3∣D=1,P=1) \times P(X=1∣P=1,H=3) =
\frac{1}{9}\times\frac{1}{2}\times(1-s)=\frac{1-s}{18}\)
\(\frac{1}{9} \times P(H=3∣D=1,P=2) \times P(X=1∣P=2,H=3) =
\frac{1}{9}\times1\times s=\frac{s}{9}\)
\(\frac{1}{9} \times P(H=2∣D=1,P=3) \times P(X=1∣P=3,H=2)=
\frac{1}{9}\times1\times s=\frac{s}{9}\)
Added up we get:
\(P(D=1,P=j,H=k,X=1)= \frac{1+s}{9}\)
But this is equal with the probabilities of the scenarios where D=X=2 and D=X=3. Knowing this, we can multiply the previous result with 3 and we will get:
\(P(D=X)=\frac{1+s}{3}\)
This is expressing the probability of winning the car using the parameter s to indicate the likelihood of switching from the initial choice. If we take the two extreme cases we will have the following results:
- The player never switches: \(P(D=X)=\frac{1}{3}\)
- The player always switches: \(P(D=X)=\frac{2}{3}\)
As you can see we made the proof that switching is always better than staying.
All I can say is Q.E.D.